M12: General Trees

Video: Download m13.70_aexp

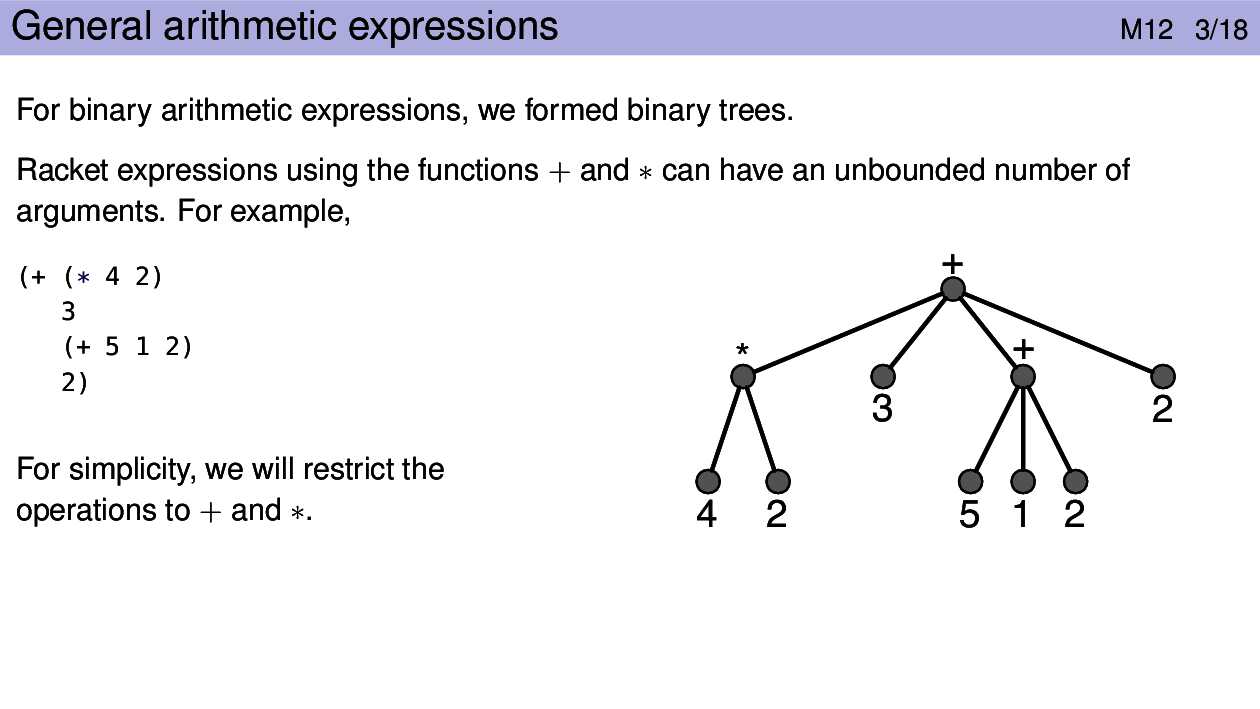
Handling any number of children needs a better solution than just adding a bunch more fields to the node structure. The simplest solution we have for handling an unknown number of things is a list.

So, we’ll put the children (subtrees) into a list.

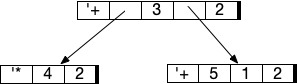
In the example, note that + at the root has four children and the subexpression (+ 5 1 2) has 3.

To evaluate this tree, we evaluate all of the subtrees (four of them!) and then apply the operator at the root (+) to those values. Note that the operator must be able to handle a variable number of children.

Remember the data definition for a binary arithmetic expression:

;; A binary arithmetic expression (BinExp) is one of:
;; * a Num
;; * a BINode

(define-struct binode (op left right))
;; A Binary arithmetic expression Internal Node (BINode)
;;     is a (make-binode (anyof '* '+ '/ '-) BinExp BinExp)

Here we stored exactly two subtrees using the left and right fields in the binode structure. One or both of could have been empty.

Now we’ll replace both of those with a list that stores exactly as many subtrees as we need.

In these examples, everything comes in pairs: two (related) data definitions, two function templates, two functions.

Note that the OpNode structure contains a list of arithmetic expressions to handle the variable number of children in the tree. That will add a little more complexity to our templates and functions. Remember the guidelines for writing templates !
Video m11.20_bt_template is also helpful.

To help visualize our data definition, lets draw on the diagrams we did earlier for lists and add a new element: structures. To represent a structure, we’ll use a rounded box for each field. Each box is labeled with the field’s name. The contents of the field will be drawn inside the box.

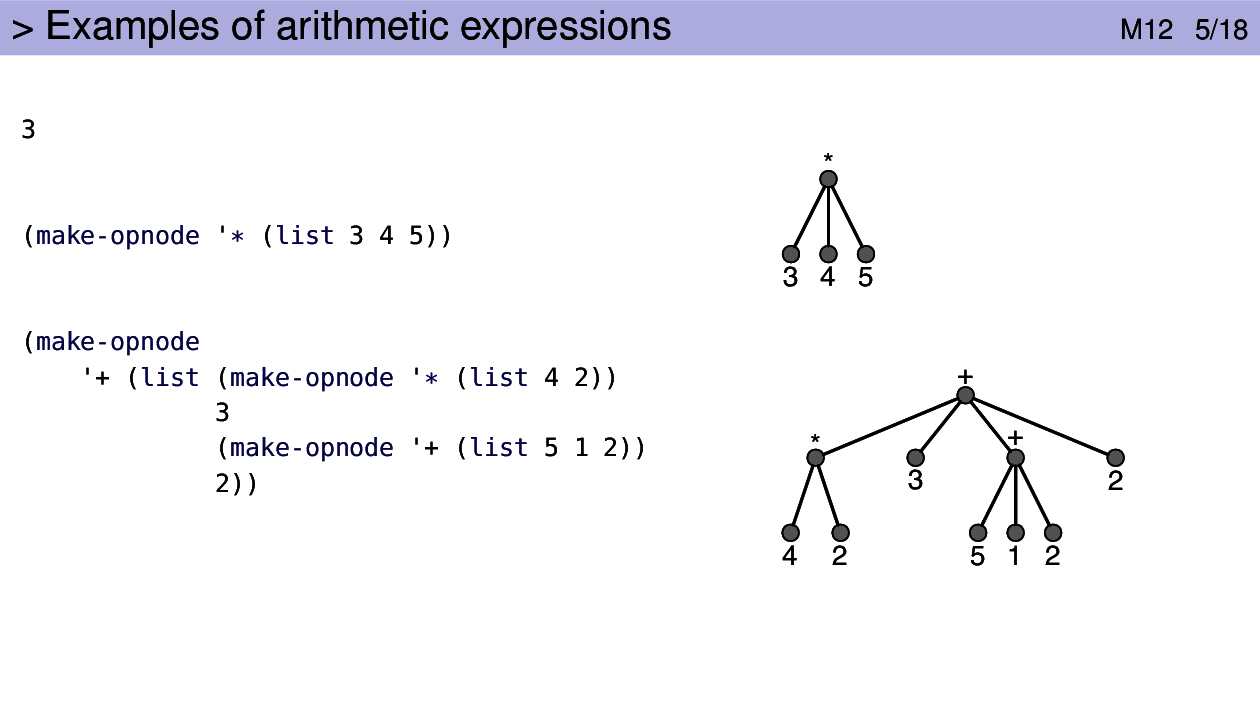
For example, here is an opnode structure corresponding to the second example. It has two fields, op and args. The contents of the first field is the '* symbol. The contents of the second field is a list of numbers.

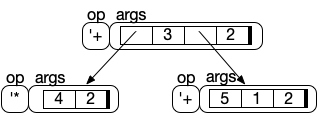
As we saw earlier , when things get complicated in our diagrams we won’t nest one structure inside another. Instead, we’ll draw an arrow to it. Here is a representation of the third example:

The point, here, is that the args field of the opnode structure contains a list. That allows us to handle a variable number of subtrees.

Be sure to watch the earlier video to see the development of this function.

The names of eval and apply are chosen deliberately because they exist in the full Racket language with similar purposes.

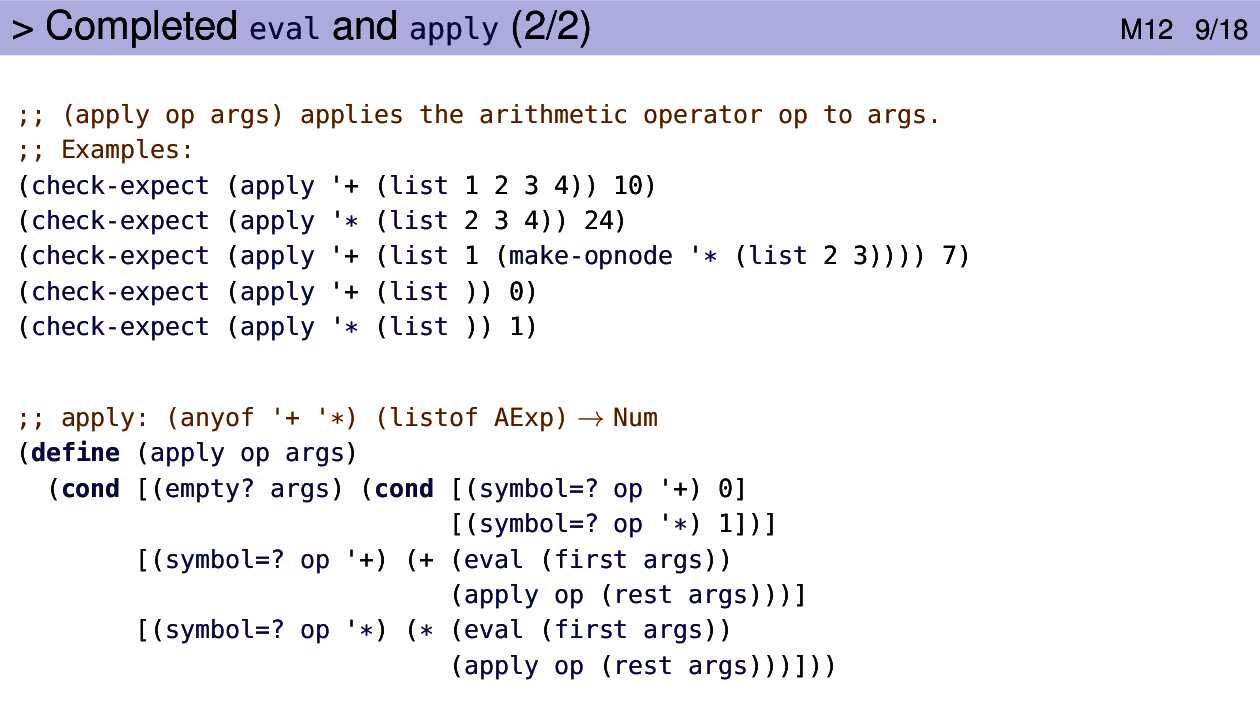
Note the examples:

• The first one is an instance of the smallest possible expression – a single number.
• The second and third involve multiple arguments, one for each operator, and are typical cases.
• The last one shows that we should be able to handle subexpressions.

Surprised by the last two tests? Watch the video !

This is a L-O-N-G trace, even in its condensed form. One approach is to just work your way through it from start to finish.

Another approach is work your way through the steps until you reach a recursive function application. Then assert the inductive hypothesis (that is, assume it will produce the correct value given its purpose). Then skip ahead and insert that value and finish the trace.

See the section on structures vs. lists .

A representation of the third example:

This data definition has only one part and is not explicitly self-referential. That may lead you to try to develop the corresponding eval function as a single function. You’re welcome to try, but trust us – it’s easier to continue to use mutual recursion. One function to handle a complete expression and another function to handle a list of expressions (plus the operator used on them). Think of the second function as a helper function if you want, but when you’re done you’ll see the mutual recursion.

We’ve run into these complex relationships quite a few times in this module and the previous two:

• A binary tree (BT) is defined in terms of a Node and a Node is defined in terms of a BT.
• A binary search tree (BST) is also defined in terms of a Node, which is defined in terms of a BST.
• A binary arithmetic expression (BinExp) is defined using a BINode, which uses BinExp.
• A general arithmetic expression (AExp) is defined in using an OpNode, which uses an AExp.

We did not need nor use mutual recursion for the binary tree and binary search tree functions we wrote.

For binary expression trees, mutual recursion again shows up naturally in the full implementation of the templates . It made use of mutual recursion under the guise of a helper function.

Until you become familiar with it, mutual recursion can be a bit of a head-scratcher. Some students try to avoid it for that reason. Don’t. Follow the process to derive the templates. Mutual recursion will appear naturally when it’s needed. Use those templates to write your functions. You might find a way to get rid of the mutual recursion, but you don’t need to. Sometimes mutual recursion is the clearest way to express the computation.

A general arithmetic expression is a situation where mutual recursion is a clear “win”. The code we developed for eval and apply is pretty easy to read and understand.

In contrast, here’s an implementation of eval that does not use mutual recursion. It was a bear to write and is a pain to read and understand. Note that it relies on an ugly trick of reconstructing the OpNode to have a shorter list of arguments.

;; (eval exp) evaluates the arithmetic expression exp.
;; eval: AExp -> Num
(define (eval exp)
  (cond [(number? exp) exp]
        [(symbol=? (opnode-op exp) '+)
         (cond [(empty? (opnode-args exp)) 0]
               [else 
                (+ (eval (first (opnode-args exp)))
                   (eval (make-opnode (opnode-op exp)
                                      (rest (opnode-args exp)))))])]
         [(symbol=? (opnode-op exp) '*)
          (cond [(empty? (opnode-args exp)) 1]
                [else
          (* (eval (first (opnode-args exp)))
             (eval (make-opnode (opnode-op exp) (rest (opnode-args exp)))))])]
         ))

Summary: Follow the templates. Use mutual recursion when it arises.

The CS135 slides are created in a typesetting program called “LaTeX”, which uses these principles. For example, the contents of a slide is identified with \begin{frame} ... \end{frame}. Different syntax, but the same idea as (list 'frame ...). Both mark the beginning and end of the stuff that makes up a frame or a chapter.

Our website is written using HTML, which is similar. Instead of (list 'title "CS135"), HTML uses tags: <title>CS135</title>.

You have the tools necessary to develop a data definition for a web page as shown on the slide. It would be more complex than the data definitions we’ve seen so far, but it’s a straight-forward extension.

Once you had that data definition, you could write a Racket program that consumes such a webpage and produces the HTML as a string.