M09: Patterns of Recursion

Towards the end of the last module we took a brief aside to discuss MergeSort. We said it’s not simple recursion. So what kind of recursion is it?

It’s what we will call “generative recursion” – one of the hardest kinds to work with.

The purpose of this module is two-fold:

1. Introduce “accumulative recursion” so you can begin to use it.
2. Help you recognize “mutual recursion” and “generative recursion” so you can avoid them until we learn more.

To identify simple recursion, look at the arguments to the recursive function application – those places where the function applies itself recursively.

(define (func lst) ... (func (rest lst)) ...) ;; Simple
(define (func lst x) ... (func (rest lst) x) ...) ;; Simple
(define (func lst x) ... (func (process lst) x) ...) ;; NOT Simple
(define (func lst x) 
 ... (func (rest lst) (math-function x)) ...) ;; NOT Simple

Need a review of the signs of simple recursion ? Follow the link.

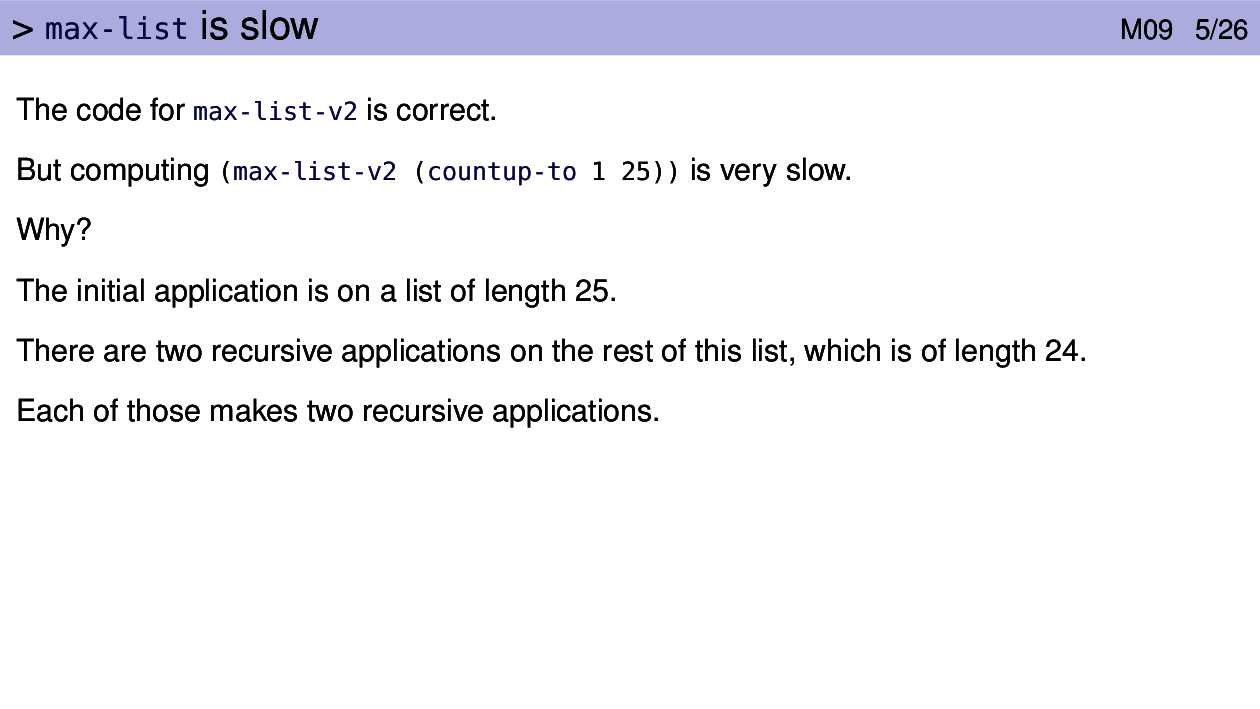
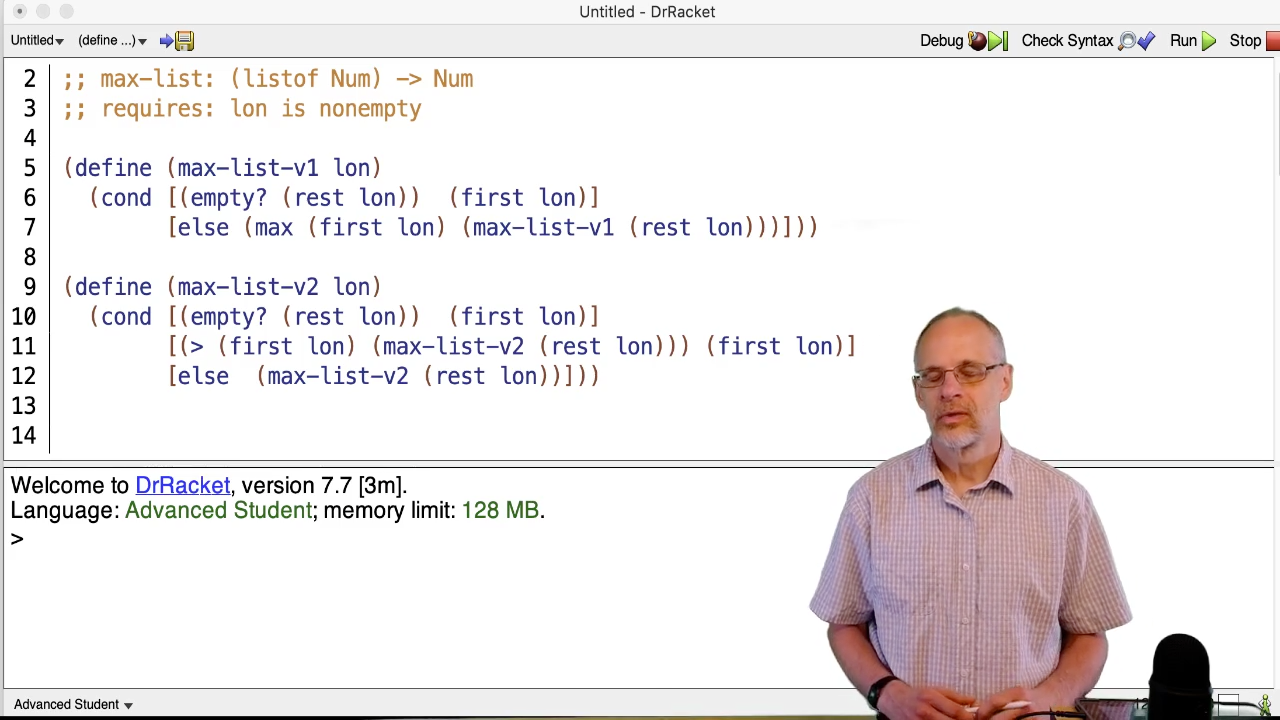
Here is the implementation of max-list that we discussed in the M06 video on non-empty lists:

(define (max-list-v1 nums)
  (cond [(empty? (rest nums)) (first nums)]
        [else (max (first nums)
                   (max-list-v1 (rest nums)))]))

It uses the built-in function max to take the maximum of the first number on the list and the number returned by processing the rest of the list recursively. It uses simple recursion and works correctly.

The version on the slide might result from the following very reasonable thought process:

The application of any function, including max, requires some overhead. Since max is so simple I’ll just write max-list using > to find the maximum of the two numbers without max function and the associated overhead.

This is a commonly used optimization called “in-lining” (usually done by computer programs like DrRacket, not humans).

In this case “in-lining” fails, massively. Watch the video to see how and why.

Video: Download m09.20_max-list

You’ve already seen many of the functions in the examples column. We’ll see binary-search in M11. mergesort (which you may have seen at the end of the previous module) is another example of O(n log₂ n).

We don’t expect you to do much with efficiency at this point. We want you to know that functions can be placed into different “families” of efficiency and that some of those families are considerably more efficient (faster) than others.

We do expect you to be able to recognize when your function applies itself recursively twice and to be able to avoid that. Note that the following code is not necessarily a problem:

(define (foo lst ...)
       ... (foo (rest lst) ...)   ;; application 1
       ... (foo (rest lst) ...)   ;; application 2
)

It’s OK if one application of (foo ...) applies foo at either application 1 or application 2. It’s a problem if one application of foo does both of them.

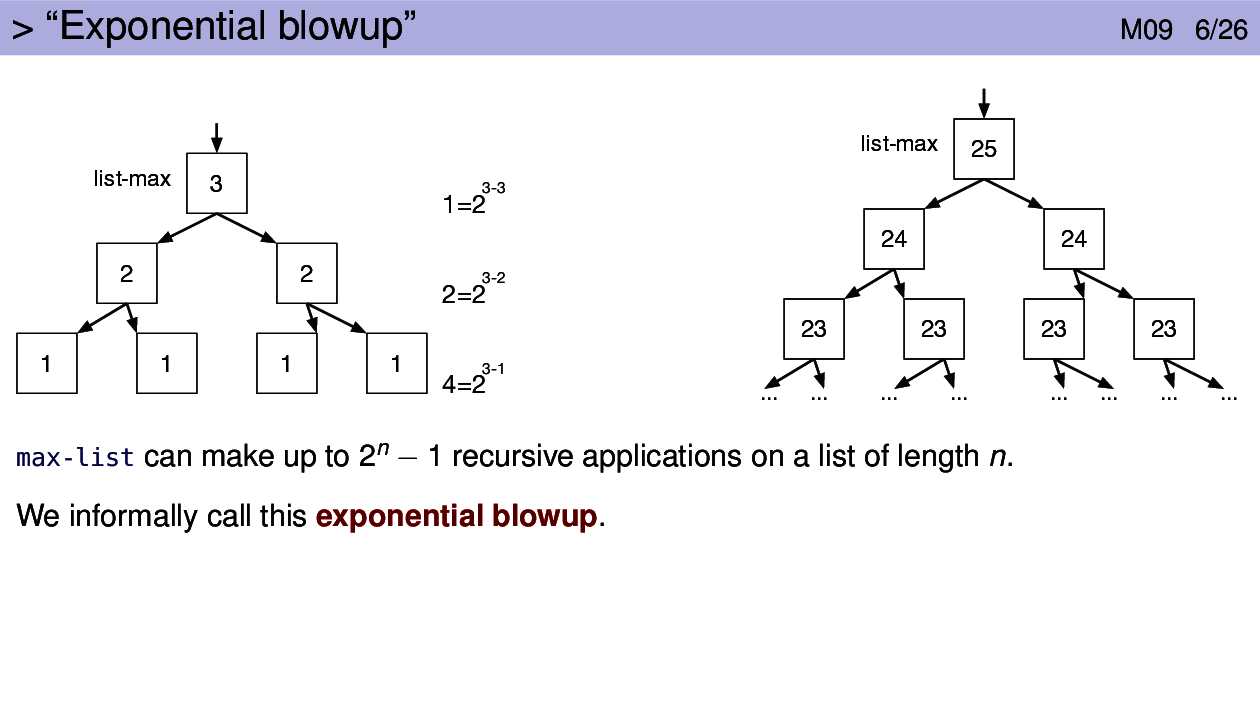
In many cases the slow version does the exact same computation twice: (max-list-v2 (rest lon)). That leads to exponential blowup.

The fast version does the computation (max-list-v1 (rest lon)) and passes that result to a helper function. The helper function can make use of that value as often as it needs to without calculating it again, thus avoiding exponential blowup.

This is a useful technique. We’ll see it again.

max-list/acc is not simple recursion! In simple recursion the arguments where max-list/acc is applied would be either one step closer to the base case or unchanged. The first argument, (rest lon), is one step closer to the base case. But the second argument is sometimes max-so-far (that is, unchanged) and sometimes (first lon). It’s that last one that kills it. (first lon) is neither one step closer to the base case nor is it unchanged. Therefore this isn’t simple recursion.

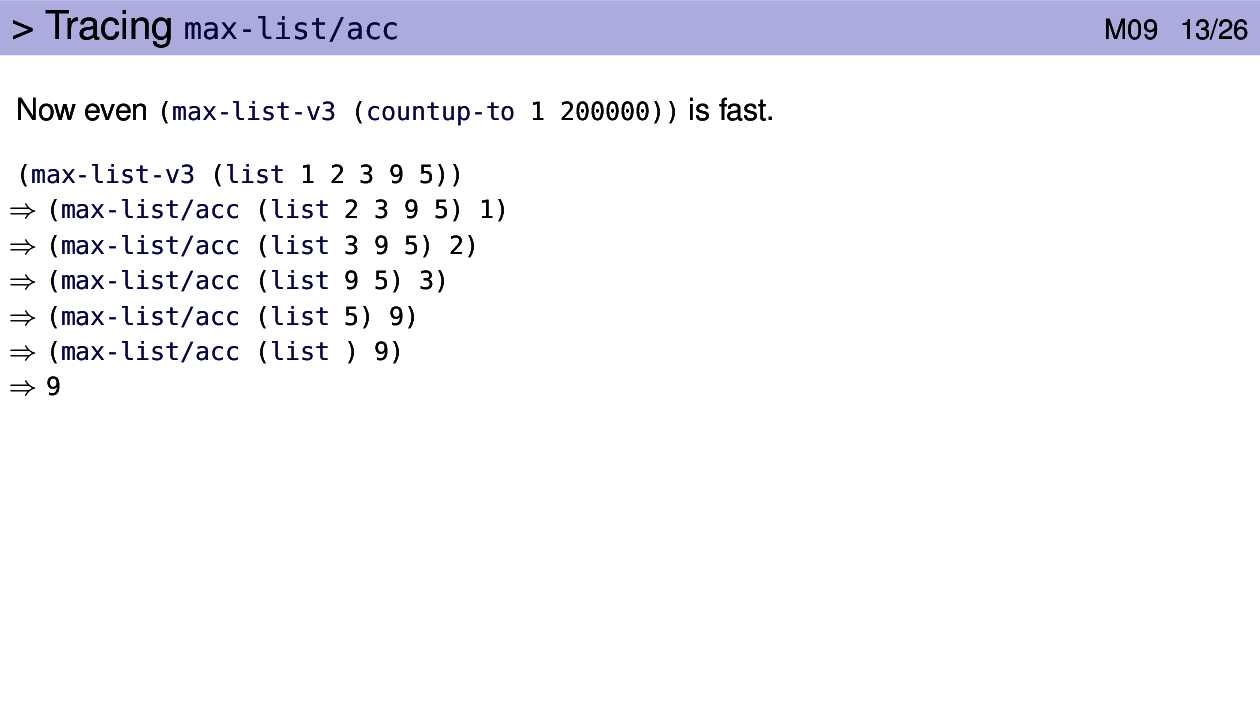
max-list-v3 is a simple wrapper around max-list/acc, which does the actual work. Wrappers are often used with accumulative recursion due to the extra parameters which need to be initialized.

The first time max-list/acc is applied the max-so-far parameter is set to 1, the first element on the list. The lon parameter is set to the rest of the list.

That first application of max-list/acc looks at the first element of lon, the remainder of the list, and realizes that it’s bigger than the maximum value seen so far. So max-list/acc is applied with that new value (2) and the rest of the list. This happens 2 more times with 3 and 9. At each stage max-so-far is the maximum value seen in the list so far.

When the first value of lon is 5, it is not bigger than max-so-far and so max-so-far is left unchanged in the next function application.

When the list is empty we’ve examined the entire list and max-so-far is the answer produced by the base case.

Simple recursion will continue to be the main tool in our programming toolbox. However, sometimes accumulative recursion will be easier or yield a more efficient or elegant solution. In such cases we strongly encourage you to use it.

Just like there are indicators to identify simple recursion, there are indicators to identify accumulative recursion.

An accumulative function requires at least one accumulator; there may be more than one.

my-reverse uses simple recursion. It does not use the double application that got max-list into trouble but is still problematic. Watch this short video for the intuition of why that’s the case and why the revision on the next slide is much better.

Video: Download m09.50_reverse

This implementation of my-reverse is a wrapper function that makes use a my-rev/acc, a helper function that does all of the real work with accumulative recursion.

You can use this code to verify that you are getting the correct answers for reasonably small values of n.

;; (fib n) Produce the n-th value in the Fibonacci sequence.
;; fib: Nat -> Nat

(define (fib n)
  (cond [(< n 2) n]
        [else (+ (fib (- n 1)) (fib (- n 2)))]))

We’ll often use mutual recursion when we write functions on general trees in M13.

This drawing by MC Escher illustrates mutual recursion well. Instead of “f applies g and g applies f”, we have “right hand draws left hand and left hand draws right hand”.

One more short video on why this is hard.

Video: Download m09.70_gcd

“Freely calculated” means that there are no constraints. Simple recursion has the constraint that the calculation must give a result that’s one step closer to the base case. Accumulative recursion has a constraint that the calculation must be closer to the solution.

With generative recursion, there are no constraints on the calculations.

In CS135, we have fairly specific criteria for simple recursion, accumulative recursion, and mutual recursion. If the algorithm is recursive and not one of those three patterns, then it must be the generative recursion pattern.